Factoriales
Un factorial se designa con un número natural positivo seguido por un
signo de exclamación (es decir 8!). El valor de un factorial es el
producto de todos los números desde 1 hasta el número del factorial. 8! =
1*2*3*4*5*6*7*8 = 40,320. Los factoriales se utilizan para determinar
las cantidades de combinaciones y permutaciones y para averiguar
probabilidades.
Ejemplo
- 4! = 4 × 3 × 2 × 1 = 24
- 7! = 7 × 6 × 5 × 4 × 3 × 2 × 1 = 5040
- 1! = 1
| n | n! | ||
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 2 × 1 | = 2 × 1! | = 2 |
| 3 | 3 × 2 × 1 | = 3 × 2! | = 6 |
| 4 | 4 × 3 × 2 × 1 | = 4 × 3! | = 24 |
| 5 | 5 × 4 × 3 × 2 × 1 | = 5 × 4! | = 120 |
| 6 | etc | etc |
Así que la regla es:
n! = n × (n-1)!
¿Que sucede con 0!?
El factorial de cero es interesante... se suele estar de acuerdo en que 0! = 1.
Parece raro que no multiplicar ningún número dé 1, pero ayuda a simplificar muchas cuestiones.
Una lista relativamente pequeña
| n | n! |
|---|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 2 |
| 3 | 6 |
| 4 | 24 |
| 5 | 120 |
| 6 | 720 |
| 7 | 5.040 |
| 8 | 40.320 |
| 9 | 362.880 |
| 10 | 3.628.800 |
| 11 | 39.916.800 |
| 12 | 479.001.600 |
| 13 | 6.227.020.800 |
| 14 | 87.178.291.200 |
| 15 | 1.307.674.368.000 |
| 16 | 20.922.789.888.000 |
| 17 | 355.687.428.096.000 |
| 18 | 6.402.373.705.728.000 |
| 19 | 121.645.100.408.832.000 |
| 20 | 2.432.902.008.176.640.000 |
| 21 | 51.090.942.171.709.400.000 |
| 22 | 1.124.000.727.777.610.000.000 |
| 23 | 25.852.016.738.885.000.000.000 |
| 24 | 620.448.401.733.239.000.000.000 |
| 25 | 15.511.210.043.331.000.000.000.000 |
¿Podemos calcular factoriales con decimales?
¿Puedes calcular factoriales de 0,5 o -3,217?
¡Sí que puedes! Pero tienes que usar algo que se llama "función Gamma", y que es mucho más complicado. Asi que llama al Maximo mas cercano que tengas para que te explique
Factorial de un medio
Lo que sí te puedo decir es que el factorial de un medio (½) es la mitad de la raíz cuadrada de pi = (½)√π, y que los factoriales de algunos "semienteros" son:
| n | n! |
|---|---|
| (-½)! | √π |
| (½)! | (½)√π |
| (3/2)! | (3/4)√π |
| (5/2)! | (15/8)√π |
Y todavía complen la regla de que "el factorial de un número es: el número por el factorial de (1 menos que el número)", por ejemplo
(3/2)! = (3/2) × (1/2)!
(5/2)! = (5/2) × (3/2)!
¿Resuelveme esta (8/2)!?(5/2)! = (5/2) × (3/2)!
Teorias combinatorias
La Teoria Combinatoria es la rama de las matematicas que se ocupa del estudio de las formas dentar. Aparte del interes que tiene en si misma, la combinatoria tiene aplicaciones de gran importancia en otras areas, y en particular a la Teoria de Probabilidades.
La Teoria Combinatoria estudia las agrupaciones que pueden ser formadas cuando se toman todos, o algunos, de los elementos de un conjunto finito. Los elementos del conjunto pueden ser de cualquier naturaleza: numeros, personas, empresas, articulos producidos por una fabrica, etc. La Teoria Combinatoria estudia especialmente el numero de agrupaciones que pueden ser obtenidas bajo algun modo de composicion de los elementos. Para ello, distingue basicamente tres conceptos:
arreglos, permutaciones y combinaciones.
En todo problema combinatorio hay varios conceptos claves que debemos distinguir:
1. Población
Es el conjunto de elementos que estamos estudiando. Denominaremos con m al número de elementos de este conjunto.
2. Muestra
Es un subconjunto de la población. Denominaremos con n al número de elementos que componen la muestra.
Los diferentes tipos de muestra vienen determinados por dos aspectos:
Orden
Es decir, si es importante que los elementos de la muestra aparezcan ordenados o no.
Repetición
La posibilidad de repetición o no de los elementos.
Factorial de un número natural
Es el producto de los “n” factores consecutivos desde “n” hasta 1. El factorial de un número se denota por n!.



Variaciones
Variaciones ordinarias
Se llama variaciones ordinarias de m elementos tomados de n en n (m ≥ n) a los distintos grupos formados por n elementos de forma que:
No entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.


También podemos calcular las variaciones mediante factoriales:


Las variaciones se denotan por 

Variaciones con repetición
Se llamann variaciones con repetición de m elementos tomados de n en n a los distintos grupos formados por n elementos de manera que:
No entran todos los elementos si m > n. Sí pueden entrar todos los elementos si m ≤ n
Sí importa el orden.
Sí se repiten los elementos.


Permutaciones
Se llama permutaciones de m elementos (m = n) a las diferentes agrupaciones de esos m elementos de forma que:
Sí entran todos los elementos.
Sí importa el orden.
No se repiten los elementos.


Permutaciones circulares
Es un caso particular de las permutaciones.
Se utilizan cuando
los elementos se han de ordenar "en círculo", (por ejemplo, los
comensales en una mesa), de modo que el primer elemento que "se sitúe"
en la muestra determina el principio y el final de muestra.

PC7= (7 − 1)! = 6! = 6 · 5 · 4 · 3 · 2 · 1 = 720
Permutaciones con repetición
Permutaciones con repetición de m elementos donde el primer elemento se repite a veces , el segundo b veces , el tercero c veces, ...(m = a + b + c + ... = n) son los distintos grupos que pueden formarse con esos m elementos de forma que :
Sí entran todos los elementos.
Sí importa el orden.
Sí se repiten los elementos.


Combinaciones
Se llama combinaciones de m elementos tomados de n en n (m ≥ n) a todas las agrupaciones posibles que pueden hacerse con los m elementos de forma que:
No entran todos los elementos.
No importa el orden.
No se repiten los elementos.


También podemos calcular las combinaciones mediante factoriales:

Las combinaciones se denotan por 

Combinaciones con repetición
Las combinaciones con repetición de m elementos tomados de n en n (m ≥ n), son los distintos grupos formados por n elementos de manera que:
No entran todos los elementos.
No importa el orden.
Sí se repiten los elementos.

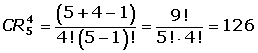
Números combinatorios
El número  se llama también número combinatorio. Se representa por
se llama también número combinatorio. Se representa por  y se lee "m sobre n".
y se lee "m sobre n".


Propiedades de los números combinatorios
1. 

2.

Los números de este tipo se llaman complementarios.
3.


El triángulo de números combinatorios de Tartaglia o de Pascal
(debido a que fue este matemático quien lo popularizó) es un triángulo
de números enteros, infinito y simétrico, del que podemos ver sus
primeras líneas:

Propiedades del Triángulo de Pascal o de Tartaglia
1.
La primera fila corresponde a los números combinatorios de 1, el número
superior es un 1, la segunda de 2, la tercera de 3 y así sucesivamente.
2.Todas la filas empiezan y acaban en 1.

3.Todas las filas son simétricas.

4.Cada número se obtiene sumando los dos que están situados sobre él.
Aplicando estas propiedades podemos escribir el triángulo de Pascal:

El triángulo de Pascal o de Tartaglia nos será muy útil para calcular los coefecientes del binomio de newton
Adminstrador: de hoy Juan Carlos Ruiz
No hay comentarios:
Publicar un comentario