Secciones Conicas

Una superficie cónica de revolución está engendrada por la rotación de una recta alrededor de otra recta fija, llamada eje, a la que corta de modo oblicuo.
Se denomina sección cónica a la curva intersección de un cono con un plano que no pasa por su vértice. Se clasifican en tres tipos: elipses, parábolas e hipérbolas.

La elipse 

Es la sección producida en una superficie cónica de revolución por un plano oblicuo al eje, que no sea paralelo a la generatriz y que forme con el mismo un ángulo mayor que el que forman eje y generatriz.

        

Elementos de la elipse:

• Focos
  

Son los puntos fijos F y F'.

• Eje focal
  

Es la recta que pasa por los focos.

• Eje secundario
  

Es la mediatriz del segmento FF'.

• Centro
  

Es el punto de intersección de los ejes.

• Ejes de simetría
  

Son las rectas que contienen al eje mayor o al eje menor.

• Centro de Simetría
  

Coincide con el centro de la elipse, que es el punto de intersección de los ejes de simetría.

Excentricidad (e) La excentricidad de la elipse es igual al cociente entre su semidistancia focal y su semieje mayor.

 

• Vertices

En el eje X

A (a,0) A´(-a,0) B (0,b) b´(0,-b)

En el eje Y

A (0,a) A´(0,-a) B (b,0) B´(-b,0)

• Focos

En el eje X

F (c,0) F´(-c,0)

En el eje Y

F (0,c) F´(0,-c)

Ecuacion de la elipse con centro (0,0)  

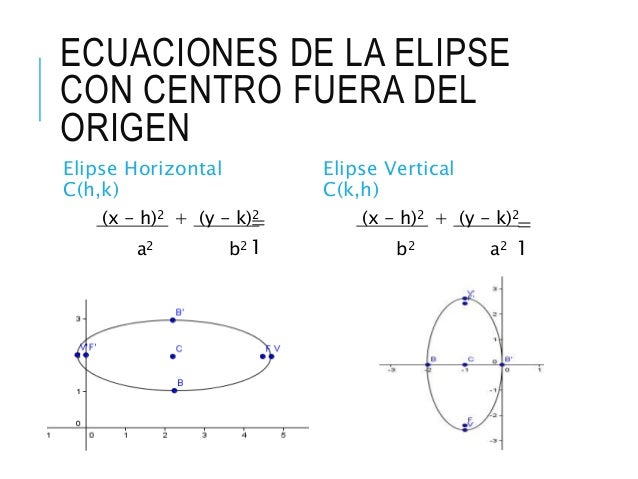
En el eje X

      

En el eje Y

 

Ecuacion de la elipse con centro (h,k) 

   

 

• Vertices

En el eje X
A (h+a,k) A´(h-a,k) B (h,b+k) B´(h,b-k)

En el eje Y

 A (h,k+a) A´(h,k-a) B (h+b,k) B´(h-b,k)

• Focos

 En el eje X

 

F (h+c,k) F´(h-c,k)

 

En el eje Y

 

F (h,k+c) F´(h,k-c)

 

  

 

Circuferencia 

Es el lugar geometrico de los puntos del plano que estan a una distancia r (radio) de otro punto llamado centro

 
 
También podemos llamar circunferencia al lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro (ver figura). La circunferencia es un caso particular de elipse.

• Ecuacion de la circunferencia 

 

En algunos casos se aplica el trinomio cuadrado perfecto

 

 

Hiperbola

 La hipérbola es la sección producida en una superficie cónica de revolución por un plano oblicuo al eje, formando con él un ángulo menor al que forman eje y generatriz, por lo que incide en las dos hojas de la superficie cónica.

 


Elementos de la Hipérbola:
 

• Vertices

En el eje X

A (a,0) A´(-a,0) B (0,b) b´(0,-b)

En el eje Y

A (0,a) A´(0,-a) B (b,0) B´(-b,0)

• Focos

En el eje X

F (c,0) F´(-c,0)

En el eje Y

F (0,c) F´(0,-c) 


Ecuación Reducida de la Hipérbola
 
Se llama ecuación reducida a la ecuación de la hipérbola cuyos ejes coinciden con los ejes coordenadas, y, por tanto, el centro de hipérbola con el origen de coordenadas.

 
Ecuación reducida de la hipérbola con los focos en el eje OY

 

 Hiperbola con centro (h,k)

 

Ecuacion

• Vertices

En el eje X
A (h+a,k) A´(h-a,k) B (h,b+k) B´(h,b-k)

En el eje Y

 A (h,k+a) A´(h,k-a) B (h+b,k) B´(h-b,k)

• Focos

 En el eje X

 

F (h+c,k) F´(h-c,k)

 

En el eje Y

 

F (h,k+c) F´(h,k-c)

Parabola

La parábola es la sección producida en una superficie cónica de revolución por un plano oblicuo al eje, siendo paralelo a la generatriz.

 

La parábola es una curva abierta que se prolonga hasta el infinito.
También podemos decir que la parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.

Elementos de la Parábola

• Foco
  

Es el punto fijo F.

• Directriz
  

Es la recta fija d.

• Parámetro
  

Es la distancia del foco a la directriz, se designa por la letra p.

• Eje
  

Es la recta perpendicular a la directriz que pasa por el foco.

• Vértice
  

Es el punto de intersección de la parábola con su eje.

• Radio vector
  

Es un segmento que une un punto cualquiera de la parábola con el foco.

Ecuación Reducida de la Parábola de Eje Horizontal
El eje de la parábola coincide con el de abscisas y el vértice con el origen de coordenadas.

Ecuación Reducida de la Parábola de Eje Vertical
El eje de la parábola coincide con el de ordenadas y el vértice con el origen de coordenadas.

Ecuación de la Parábola con Eje Horizontal Parábola con eje paralelo a OX y vértice distinto al origen.

Ecuación de la Parábola con Eje Vertical
Parábola con eje paralelo a OY, y vértice distinto al origen.